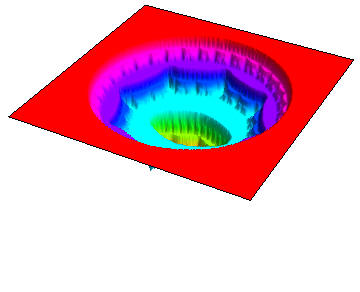
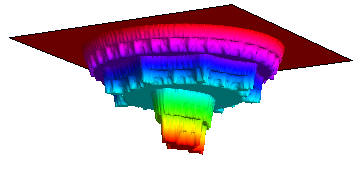
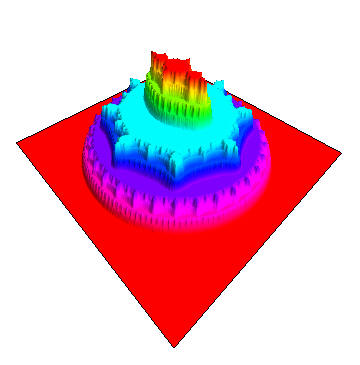
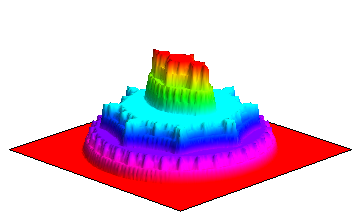
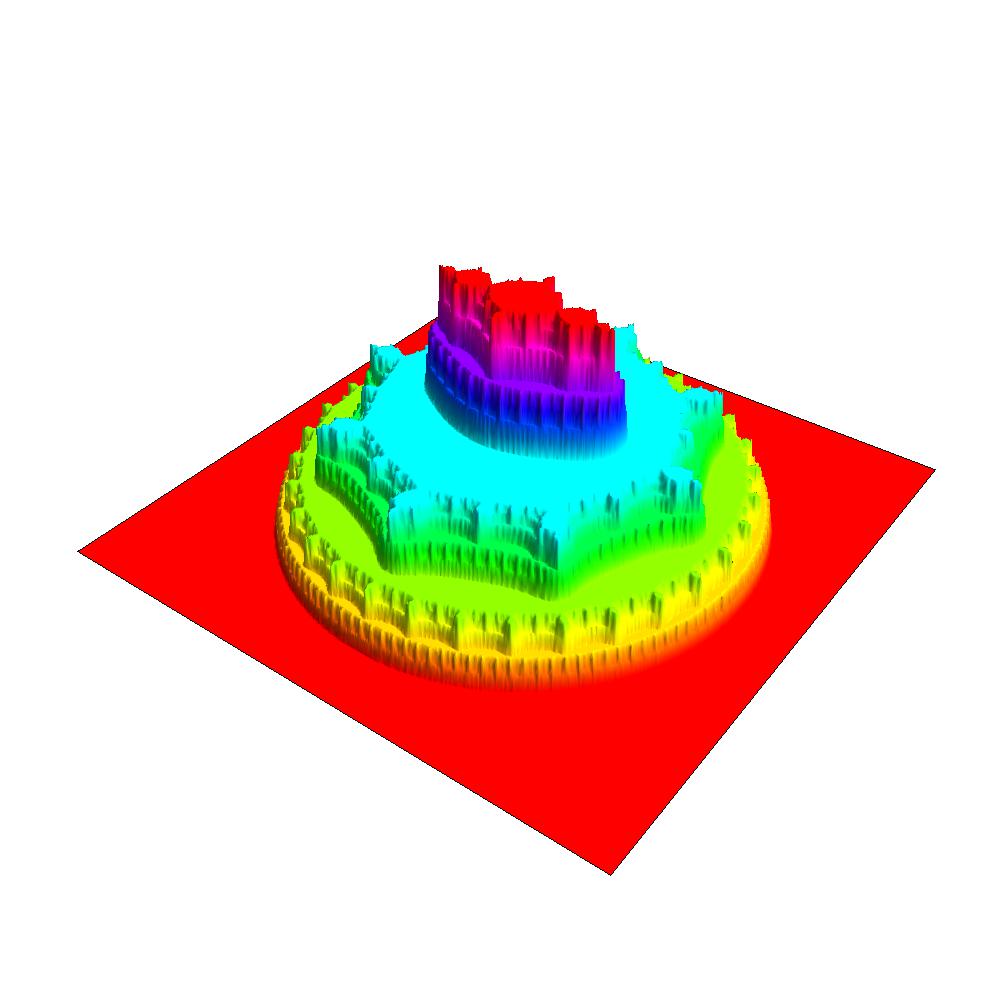
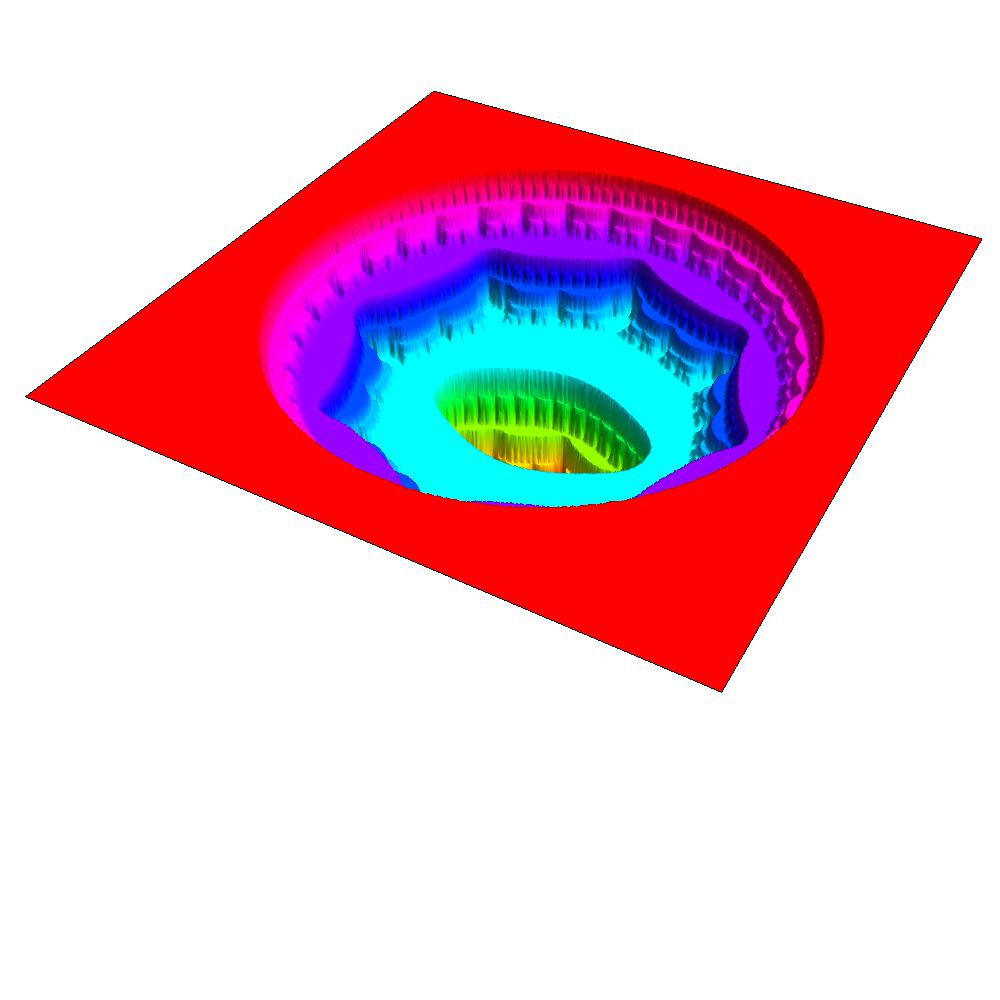
Below you will find many pictures of the so-called Devil's Collosseum. These pictures show various angles the graph of the function P(z) which is continuous on the entire complex plane, but which is flat almost everywhere (and thus is a 2-D version of the well-known Devil's Staircase). The function P(z) varies only on a thin, fractal set known as the Julia set of the associated semigroup < f, g >. The function P(z) is defined to be the probability that a random orbit under the maps f and g will converge to infinity. In this case we take f to be the second iterate of h(z) = z^2 -1 and g to be the second iterate of k(z) = z^/4. These pictures and the study of the Julia set was first conducted by Hiroki Sumi.







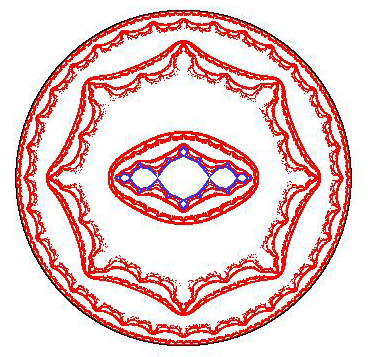
This is the Julia set of the semigroup < f, g >. It is the set on which the function P(z) seen above varies.